Interpreting neurons in an LSTM network
By Tigran Galstyan and Hrant Khachatrian.
A few months ago, we showed how effectively an LSTM network can perform text transliteration.
For humans, transliteration is a relatively easy and interpretable task, so it’s a good task for interpreting what the network is doing, and whether it is similar to how humans approach the same task.
In this post we’ll try to understand: What do individual neurons of the network actually learn? How are they used to make decisions?
Contents
- Transliteration
- Network architecture
- Analyzing the neurons
- Visualizing LSTM cells
- Concluding remarks
Transliteration
About half of the billions of internet users speak languages written in non-Latin alphabets, like Russian, Arabic, Chinese, Greek and Armenian. Very often, they haphazardly use the Latin alphabet to write those languages.
Привет: Privet, Privyet, Priwjet, …
كيف حالك: kayf halk, keyf 7alek, …
Բարև Ձեզ: Barev Dzez, Barew Dzez, …
So a growing share of user-generated text content is in these “Latinized” or “romanized” formats that are difficult to parse, search or even identify. Transliteration is the task of automatically converting this content into the native canonical format.
Aydpes aveli sirun e.: Այդպես ավելի սիրուն է:
What makes this problem non-trivial?
-
Different users romanize in different ways, as we saw above. For example,
vorwcould be Armenianվ. -
Multiple letters can be romanized to the same Latin letter. For example,
rcould be Armenianրorռ. -
A single letter can be romanized to a combination of multiple Latin letters. For example,
chcould be Cyrillicчor Armenianչ, butcandhby themselves are for other letters. -
English words and translingual Latin tokens like URLs occur in non-Latin text. For example, the letters in
youtube.comorMSFTshould not be changed.
Humans are great at resolving these ambiguities. We showed that LSTMs can also learn to resolve all these ambiguities, at least for Armenian. For example, our model correctly transliterated es sirum em Deep Learning into ես սիրում եմ Deep Learning and not ես սիրում եմ Դեեփ Լէարնինգ.
Network architecture
We took lots of Armenian text from Wikipedia and used probabilistic rules to obtain romanized text. The rules are chosen in a way that they cover most of the romanization rules people use for Armenian.
We encode Latin characters as one-hot vectors and apply character level bidirectional LSTM. At each time-step the network tries to guess the next character of the original Armenian sentence. Sometimes a single Armenian character is represented by multiple Latin letters, so it is very helpful to align the romanized and original texts before giving them to LSTM (otherwise we should use sequence-to-sequence networks, which are harder to train). Fortunately we can do the alignment, because the romanized version was generated by ourselves. For example, dzi should be transliterated into ձի, where dz corresponds to ձ and i to ի. So we add a placeholder character in the Armenian version: ձի becomes ձ_ի, so that now z should be transliterated into _. After the inference we just remove _s from the output string.
Our network consists of two LSTMs (228 cells) going forward and backward on the Latin sequence. The outputs of the LSTMs are concatenated at each step (concat layer), then a dense layer with 228 neurons is applied on top of it (hidden layer), and another dense layer (output layer) with softmax activations is used to get the output probabilities. We also concatenate the input vector to the hidden layer, so it has 300 neurons. This is a more simplified version of the network described in our previous post on this topic (the main difference is that we don’t use the second layer of biLSTM).
Analyzing the neurons
We tried to answer the following questions:
- How does the network handle interesting cases with several possible outcomes (e.g.
r=>րvsռetc.)? - What are the problems particular neurons are helping solve?
How does “t” become “ծ”?
First, we fixed one particular character for the input and one for the output.
For example we are interested in how t becomes ծ (we know t can become տ, թ or ծ). We now that it usually happens when t appears in a bigram ts, which should be converted to ծ_.
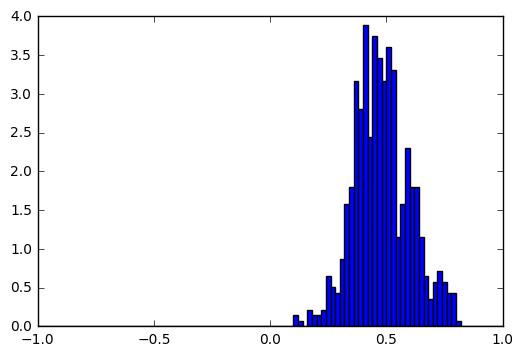
For every neuron, we draw the histograms of its activations in cases where the correct output is ծ, and where the correct output is not ծ. For most of the neurons these two histograms are pretty similar, but there are cases like this:
Input = t, Output = ծ |
Input = t, Output != ծ |
|---|---|
 |
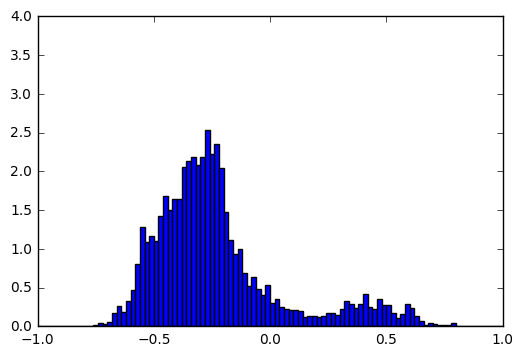 |
These histograms show that by looking at the activation of this particular neuron we can guess with high accuracy whether the output for t is ծ. To quantify the difference between the two histograms we used Hellinger distance (we take the minimum and maximum values of neuron activations, split the range into 1000 bins and apply discrete Hellinger distance formula on two histograms). We calculated this distance for all neurons and visualized the most interesting ones in a single image:
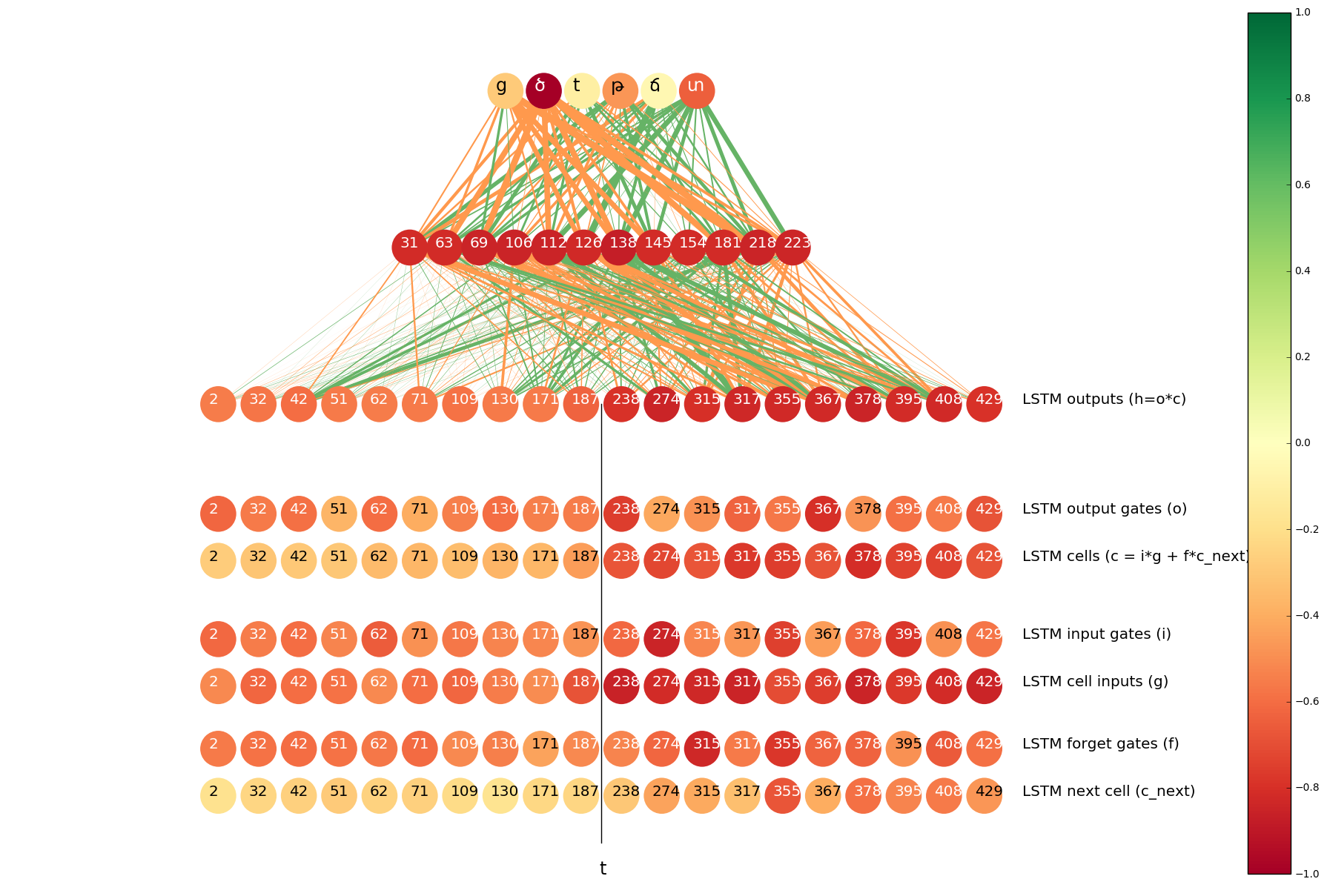
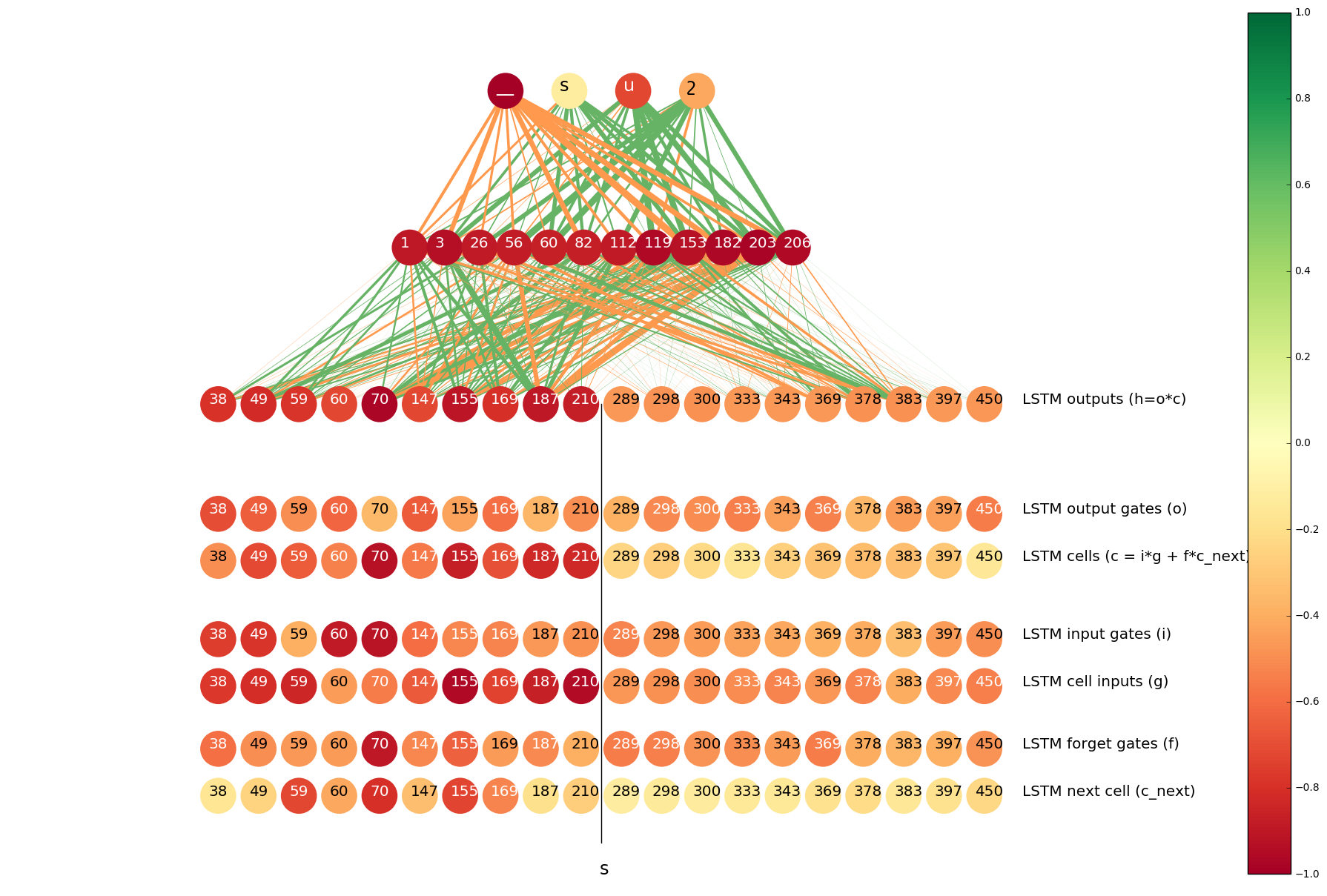
The color of a neuron indicates the distance between its two histograms (darker colors correspond to larger distances). The width of a line between two neurons indicate the mean of the value that the neuron on the lower end of the connection contributes to the neuron on the higher end. Orange and green lines correspond to positive and negative signals, respectively.
The neurons at the top of the image are from the output layer, the neurons below the output layer are from the hidden layer (top 12 neurons in terms of the distance between histograms). Concat layer comes under the hidden layer. The neurons of the concat layer are split into two parts: the left half of the neurons are the outputs of the LSTM that goes forward on the input sequence and the right half contains the neurons from the LSTM that goes backwards. From each LSTM we display top 10 neurons in terms of the distance between histograms.
In the case of t => ծ, it is obvious that all top 12 neurons of the hidden layer pass positive signals to ծ and ց (another Armenian character that is often romanized as ts), and pass negative signals to տ, թ and others.
We can also see that the outputs of the right-to-left LSTM are darker, which implies that these neurons “have more knowledge” about whether to predict ծ. On the other hand, the lines between those neurons and the hidden layer are thicker, which means that they have more contribution in activating the top 12 neurons in the hidden layer. This is a very natural result, because we know that t usually becomes ծ when the next symbol is s, and only the right-to-left LSTM is aware of the next character.
We did the same analysis for the neurons and gates inside the LSTMs. The results are visualized as six rows of neurons at the bottom of the image. In particular, it is interesting to note that the most “confident” neurons are the so called cell inputs. Recall that cell inputs, as well as all the gates, depend on the input at the current step and the hidden state of the previous step (which is the hidden state at the next character as we talk about the right-to-left LSTM), so all of them are “aware” of the next s, but for some reason cell inputs are more confident than others.
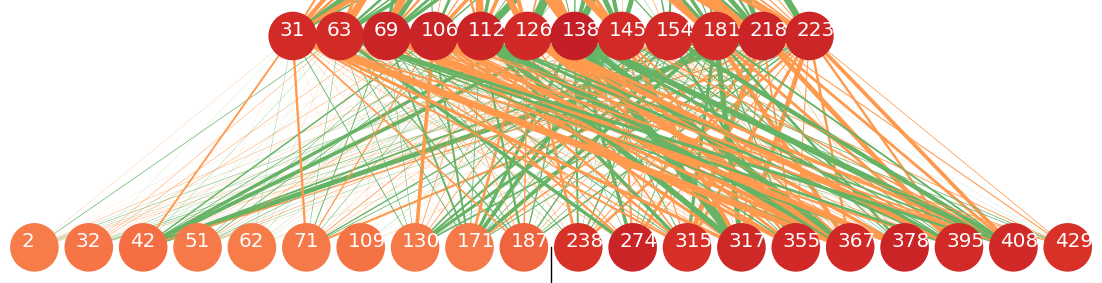
In the cases where s should be transliterated into _ (the placeholder), the useful information is more likely to come from the LSTM that goes forward, as s becomes _ mainly in case of ts => ծ_. We see that in the next plot:
What did this neuron learn?
In the second part of our analysis we tried to figure out in which ambiguous cases each of the neurons is most helpful. We took the set of Latin characters that can be transliterated into more than one Armenian letters. Then we removed the cases where one of the possible outcomes appears less than 300 times in our 5000 sample sentences, because our distance metric didn’t seem to work well with few samples. And we analyzed every fixed neuron for every possible input-output pair.
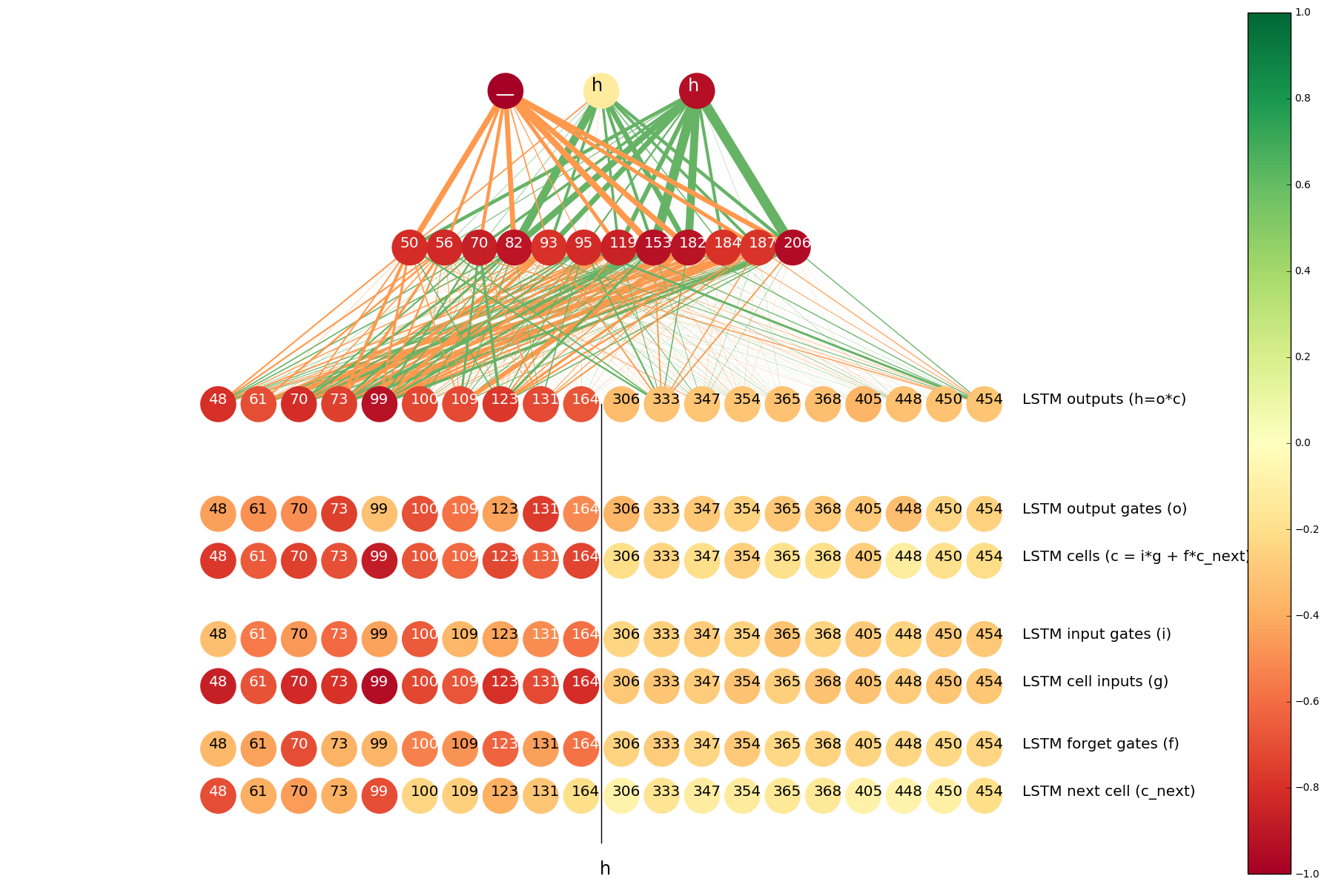
For example, here is the analysis of the neuron #70 of the output layer of the left-to-right LSTM. We have seen in the previous visualization that it helps determining whether s should be transliterated into _. We see that the top input-output pairs for this neuron are the following:
| Hellinger distance | Latin character | Armenian character |
|---|---|---|
| 0.9482 | s | _ |
| 0.8285 | h | հ |
| 0.8091 | h | _ |
| 0.6125 | o | օ |
So this neuron is most helpful when predicting _ from s (as we already knew), but it also helps to determine whether Latin h should be transliterated as Armenian հ or the placeholder _ (e.g. Armenian չ is usually romanized as ch, so h sometimes becomes _).
We visualize Hellinger distances of the histograms of neuron activations when the input is h and the output is _, and see that the neuron #70 is among the top 10 neurons of the left-to-right LSTM for the h=>_ pair.
Visualizing LSTM cells
Inspired by this paper by Andrej Karpathy, Justin Johnson and Fei-Fei Li, we tried to find neurons or LSTM cells specialised in some language specific patterns in the sequences. In particular, we tried to find the neurons that react most to the suffix թյուն (romanized as tyun).

The first row of this visualization is the output sequence. Rows below show the activations of the most interesting neurons:
- Cell #6 in the LSTM that goes backwards,
- Cell #147 in the LSTM that goes forward,
- 37th neuron in the hidden layer,
- 78th neuron in the concat layer.

We can see that Cell #6 is active on tyuns and is not active on the other parts of the sequence. Cell #144 of the forward LSTM behaves the opposite way, it is active on everything except tyuns.
We know that t in the suffix tyun should always become թ in Armenian, so we thought that if a neuron is active on tyuns, it may help in determining whether the Latin t should be transliterated as թ or տ. So we visualized the most important neurons for the pair t => թ.
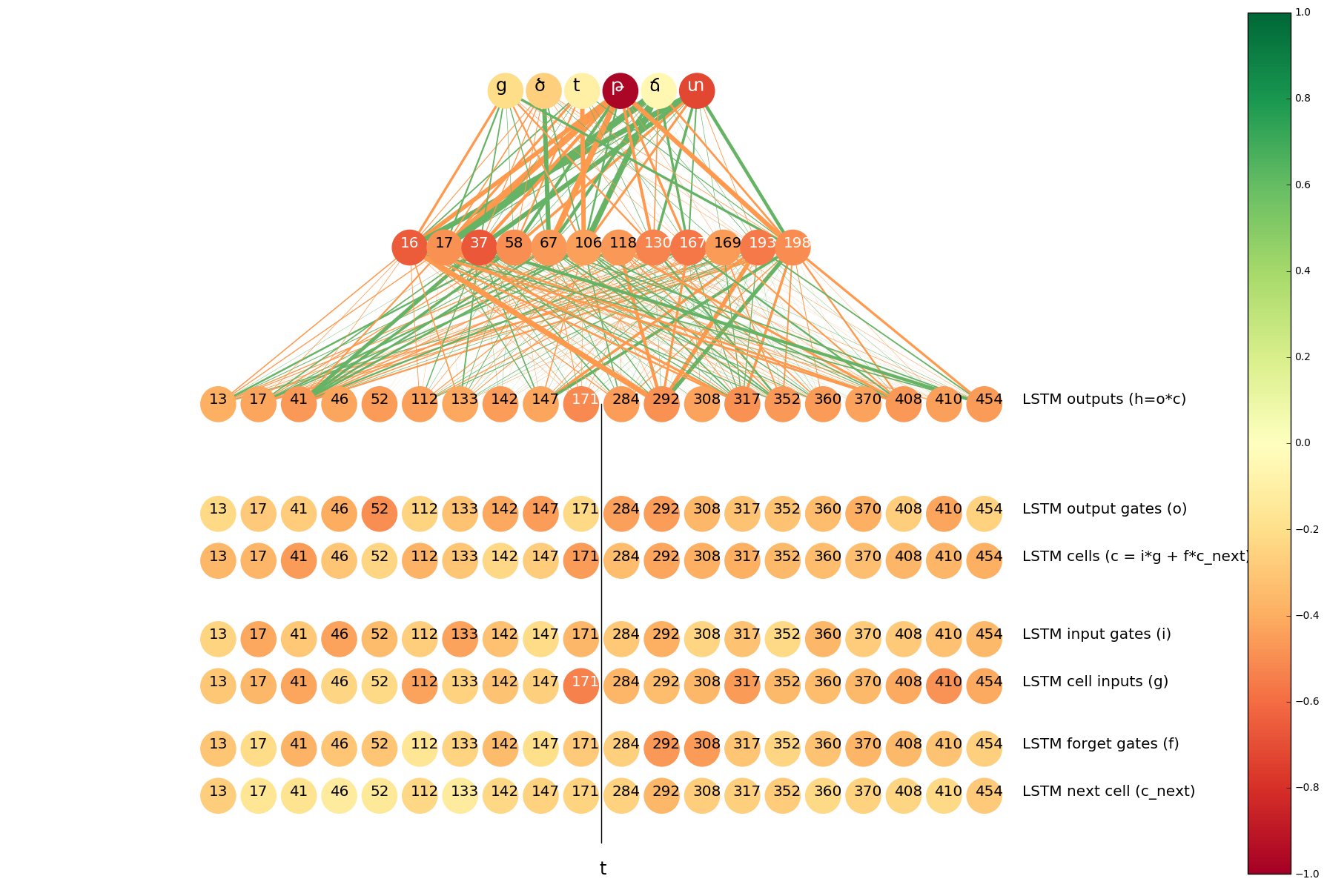
Indeed, Cell #147 in the forward LSTM is among the top 10.
Concluding remarks
Interpretability of neural networks remains an important challenge in machine learning. CNNs and LSTMs perform well for many learning tasks, but there are very few tools to understand the inner workings of these systems. Transliteration is a pretty good problem for analyzing the impact of particular neurons.
Our experiments showed that too many neurons are involved in the “decision making” even for the simplest cases, but it is possible to identify a subset of neurons that have more influence than the rest. On the other hand, most neurons are involved in multiple decision making processes depending on the context. This is expected, since nothing in the loss functions we use when training neural nets forces the neurons to be independent and interpretable. Recently, there have been some attempts to apply information-theoretic regularization terms in order to obtain more interpretability. It would be interesting to test those ideas in the context of transliteration.
We would like to thank Adam Mathias Bittlingmayer and Zara Alaverdyan for helpful comments and discussions.